<< Click to Display Table of Contents >> Navigation:  Explore Program > Belt Analyst > Drag Calculations > Pipe Conveyor Calculation > Indeterminate Analysis - Force and Deflection

Self-loading plus the various pressures due to gravity and curves results in none uniform cylindrical bending. And the contact area of two cylinders creates an elliptical indentation area. This contact area is quite important for the calculation of rubber indentation losses.

Large displacement bending arcs require ‘Elastica’ mathematical solutions; a theory of mechanics of solid materials developed by Leonhard Euler that allows for very large scale elastic deflections of structures. Contact shape is elliptical with solution extended from contact between two cylinders (pipe and roll) shown in Figure 7. These solutions require calculation of arcs between adjacent rolls using two cantilever beams joined at their fixed ends and the use elliptical integral solutions for the differential equations.

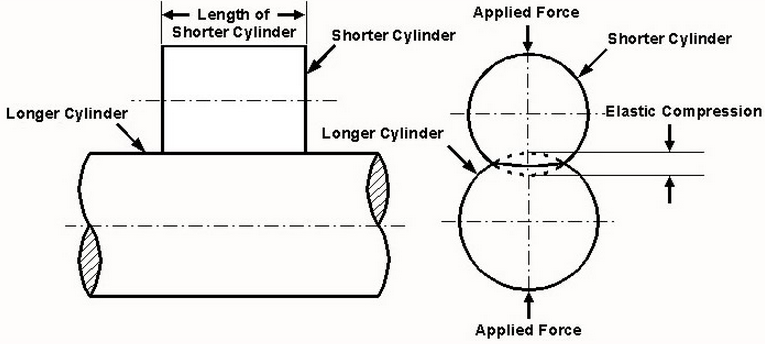
Figure 7

Modifications have been to Belt Analyst™ v 14.4.0 released in June 2015 and further modifications will be made in upcoming releases. If you compare old files, you will find the demand power requirements will almost always be greater than previous versions.

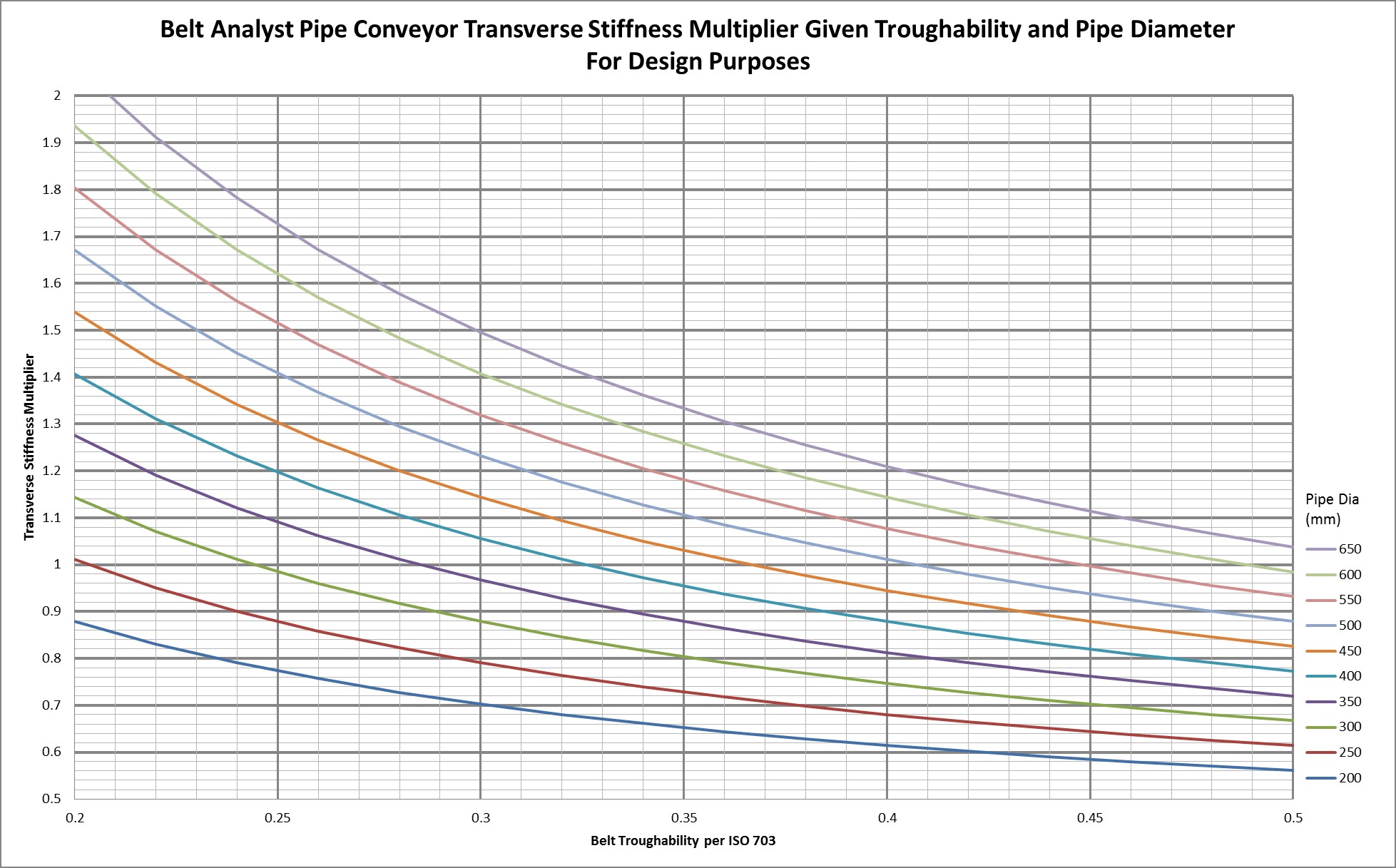
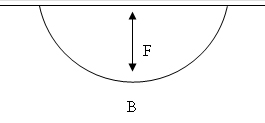
For now, troughability per ISO 703:2007 is used as a rough estimate of belt bending stiffness- Ei or Flexural Rigidity. Troughability is the ratio of F/B of belt hanging under its own weight. This could be otherwise defined as the belts natural radius.

Potential problems with this approach are:

1.Belts are not always symmetrical through thickness

2.Belts can change over time due to repeated flexure

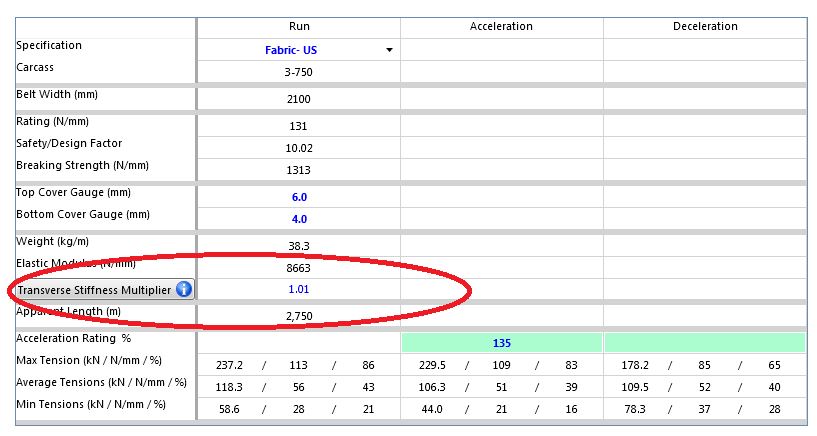
A input has been added to Belt Analyst™ in the belt folder called “Belt Transverse Stiffness Multiplier”. This will always be defaulted to 1.00 but users should always get the troughability number from the ISO 703 test from your belt manufacturer and select the appropriate stiffness multiplier for your pipe diameter per the following table.